Counting polybar polyominoes
On 2025-06-25, Jacob Siehler tooted that there are exactly 100 bilaterally symmetric regions you can build out of a complete set of the five free tetrominoes.

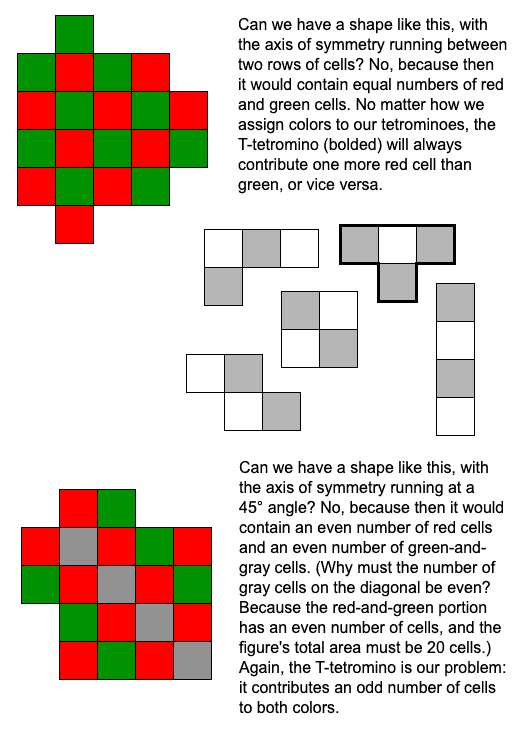
Notice that all 100 of these shapes have an odd number of rows, with the line of symmetry running orthogonally through the middle of a row. Siehler explains that a checkerboard argument rules out bilaterally symmetric shapes with an even number of rows, and even rules out shapes with the axis of symmetry running diagonally:
On the SeqFan mailing list, Victor Miller asked about the generalization: How many symmetric connected regions can you build from the complete set of \(n\)-ominoes? For \(n\)=1, 2, or 3, the answer is “one” (notice the axis of symmetry is diagonal for \(n=3\)):
..c
A BB .Cc
CCc
For \(n=4\), Siehler has computed that the answer is “100.” For \(n=5\), the problem seems completely intractable: a complete set of pentominoes occupies 60 cells, so we’d be counting a subset of the hexacontominoes. (In 2023, John Mason calculated that there are 2150182610161041739167164220 distinct free pentacontominoes. Mind you, “only” 62607290936271 of those have bilateral symmetry. But we’re talking about 60-cell animals, not 50-cell, and we also have to determine how many of those trillions or quadrillions of animals have 12-pentomino tilings.)
| n | Cells in a complete set | Animals with that number of cells | Animals buildable from a complete set | Bilaterally symmetric animals | Bilaterally symmetric animals buildable from a complete set |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 1 | 1 | 1 | 1 |
| 3 | 6 | 35 | 11 | 10 | 1 |
| 4 | 20 | 2870671950 | 3721336 | 87136 | 100 |
| 5 | 60 | \(\gg 2.15\times 10^{27}\) | ??? | \(\gg 6.26\times 10^{13}\) | ??? |
| 6 | 210 | ??? | ??? | ??? | ??? |
Okay, forget bilateral symmetry, and forget complete sets of \(p\)-ominoes. Let’s generalize in a different direction. The OEIS has a sequence counting how many regions you can build from \(n\) monominoes — that’s A000105, the number of polyominoes of size \(n\). And A056785 counts the number of regions you can build from \(n\) dominoes (the number of polydominoes of size \(n\)). What about polytrominoes, polytetrominoes, and so on, in general?
For simplicity, let’s restrict our generalization to count the shapes we can build out of \(n\) identical straight \(p\)-ominoes. I suggest that the straight \(p\)-omino can be called the “bar” of order \(p\); then the shapes we’re counting are the polybars of order \(p\). The polybars of order 1 are exactly the polyominoes. The polybars of order 2 are exactly the polydominoes. The OEIS as yet has no information on polybars of order 3 and higher. Surprisingly, neither do Miroslav Vicher’s polyforms page nor Michael Keller’s polyforms page.
There are six dibars of order 3:
XXX XXX XXXY Y
XXX YYY YYY Y XXXY
YYY XXXYYY Y Y
I marked the component bars in the diagrams above. But just as with polyominoes and polydominoes, we don’t actually care how the bars are arranged internally:
ABC ABB ABC ACCare two distinct domino tilings of a single tridomino, not two different tridominoes.
There are 55 tribars of order 3:
......X ......X .....X .....X ....X ....X ....XXX ...X... X...X
......X XXXXXXX ..XXXX XXX..X .XXXX XXX.X ..XXX.. ...X... XXXXX
XXXXXXX ......X XXX..X ..XXXX XXX.X .XXXX XXX.... XXXXXXX X...X
...X... ...X ...X... ...XX ...XX ...XXX ...XXXX ..XXX X...X XXX
...XXXX XXXX XXXXXXX ...XX XXXXX ..XXX. ...X... XXX.. X...X XXX
XXXX... XXXX ...X... XXXXX ...XX XXX... XXXX... ..XXX XXXXX XXX
.....X .....X ....X. ....X ....X ....X ....X ....X ....X ...X..
.....X .....X ....X. ....X ....X ...XX ...XX X...X XXXXX ...X..
.....X ..XXXX ....X. .XXXX XXX.X ...XX XXXXX XXXXX ...XX XXXX..
XXXXXX XXX... XXXXXX XXX.. ..XXX XXXX. ...X. X.... ...X. ...XXX
....X ....X ....X ....X ...X ..X ..X ..X ..XXX.. ..XXX. ...XXX
....X ....X ....X ....X ...X ..X .XX X.X XXX.XXX XXXXXX XXXXXX
....X ...XX XXXXX XXXXX X..X XXX XXX XXX
..XXX XXXX. ...X. X.... XXXX XX. XX. XX. .....XXX ....XXX
XXX.. ...X. ...X. X.... X... XX. X.. .X. XXXXXX.. XXXXXX.
...X ...X ...X ...X. ...X ...X ...X ...X. ...X ..X .X. X.X
...X ...X ...X ...X. ...X ...X X..X XXXX. XXXX XXX XXX X.X
...X ...X XXXX XXXX. XXXX XXXX X..X ...X. ...X XXX XXX X.X
XXXX XXXX .X.. ..XXX .XXX XXX. XXXX ..XXX .XXX XX. X.X XXX
...X X... .X..
...X X... .X.. XXXXXXXXX
The total count of \(n\)-bars of order \(p\) is:
n=1 2 3 4 5 6 7 8 9 10
monobars tribars pentabars heptabars nonabars
dibars tetrabars hexabars octabars decabars
p=1: 1 1 2 5 12 35 108 369 1285 4655
2: 1 4 23 211 2227 25824 310242 3818983 47752136 604425323
3: 1 6 55 833 14378 269710 5221076 103352306
4: 1 7 93 1973 47161 1204744 31711028 852689953
5: 1 9 144 3913 118842 3851349 128587175
6: 1 10 204 6809 252797 9951844 403553930
7: 1 12 277 10938 478377 22178331
8: 1 13 359 16427 830085 44325651
9: 1 15 454 23577 1348694 81527962
10: 1 16 558 32491 2079909 140441453
As mentioned, the first row of this table is OEIS A000105; the second row is A056785. None of the other rows or columns appear in the OEIS, although the second column has a simple closed form. I computed these numbers with a C++ program which you can find here.
