Today I discovered a little book called Sudoku Stories (Oscar Seurat, 2014). Each page presents a little encyclopedia entry on some random topic accompanied by a sudoku puzzle whose pre-filled cells trace out a shape corresponding to the entry. For example:

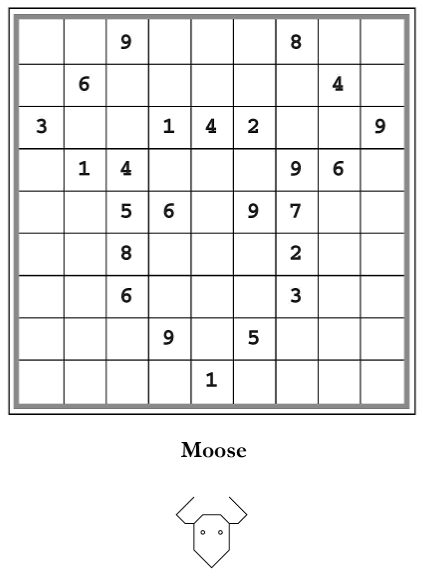
This got me thinking: There are 2⁸¹ different “images” possible on a 9x9 grid. For some of these images (e.g. the all-filled-in image, the moose image), it’s clearly possible to create a sudoku from them. For others (e.g. any image containing fewer than 17 pixels), it’s clearly impossible.

Roughly how many “sudoku-able” 9x9 images exist? Is it on the order of 2⁸¹? On the order of 2³⁰?

We can imagine a “meta-sudoku” version of the moose puzzle. Given only the moose image,

I ask you to assign numbers to the black squares so that the resulting grid is a valid sudoku puzzle (with only one possible completion, of course).

One solution to the moose meta-puzzle is Seurat’s original moose puzzle.

Does the moose meta-puzzle have a unique solution? (Trivially, no, because you can always e.g. substitute 1 for 9 and 9 for 1, to produce another valid sudoku. But does it have a unique solution up to swaps of that kind?)

Off the top of my head, I suspect that the moose meta-puzzle does not have a unique solution. Can you come up with any meta-puzzle that does have a unique solution (up to swaps)?

How many of the 2⁸¹ metapuzzles have unique solutions?