Previously on this blog: the notion of a “meta-sudoku” puzzle as a configuration of 81 squares, each labeled “filled” or “unfilled.” The goal of the puzzle is to find an assignment of numbers to the “filled” squares so that the resulting (partially filled) grid is a solvable Sudoku puzzle.

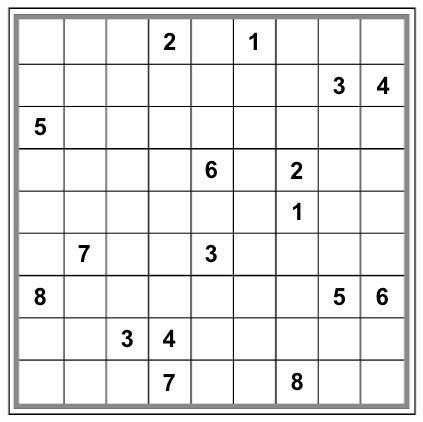
I wrote a little program to run through all the possible assignments to the following configuration:

First, I asked my program how many viable assignments existed. By “viable,” I just mean that the assignment is unique up to permutation, and it doesn’t contain any obvious contradictions out of the gate. For example: The grid below left is not viable because you can swap all the 1s for 2s (and vice versa) to create a “lower-numbered” grid. The grid below right is not viable because it contains an obvious contradiction: two 1s in the top row.

According to my program, there are 2,659,328,730 viable assignments. To compute just this number of possible assignments, without inspecting the resulting grids for solvability, took my program 67 seconds.

Note in passing that if we completely brute-forced it, by testing all 9¹⁷ possible assignments for viability, we’d have to test 9¹⁷ = 16,677,181,699,666,569 assignments! Even if we could test assignments for viability at the astonishing rate of four per nanosecond, it would still take us 48 days of continuous computation in order to test all 9¹⁷ of them. So short-circuiting large swaths of the search space turns out to be super important here.

---

Now how about validating that an assignment is a valid Sudoku — which boils down to Sudoku-solving?

On my dual-core, hyperthreaded MacBook, my program can test grids for solvability at the rate of about 50,000 grids per second. At this rate, it takes something like 15 hours of continuous computation to inspect all 2.6 billion possible viable assignments for just this one meta-sudoku configuration. So I did that — at least, long enough for it to find some solutions.

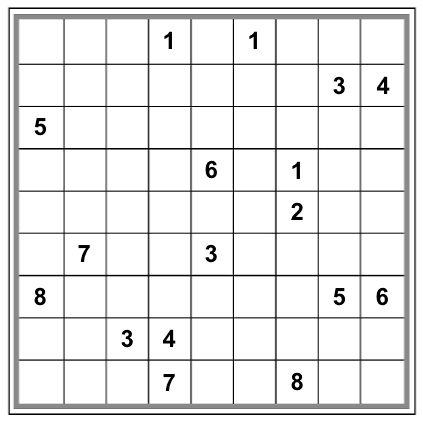
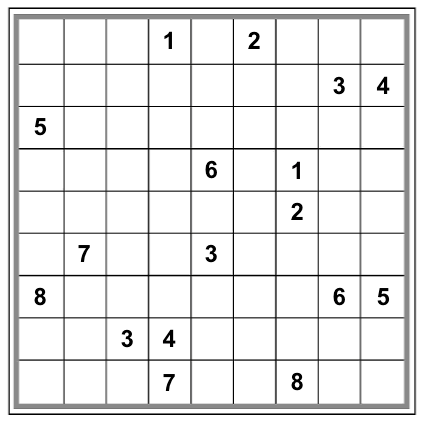
It turns out that this configuration can be filled in to create a valid Sudoku grid in at least these four fundamentally different ways:

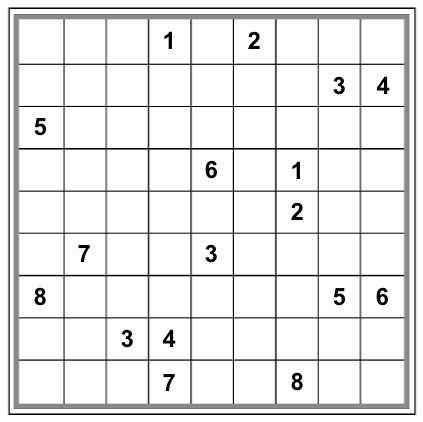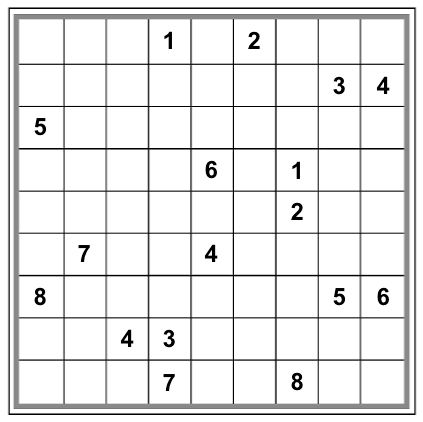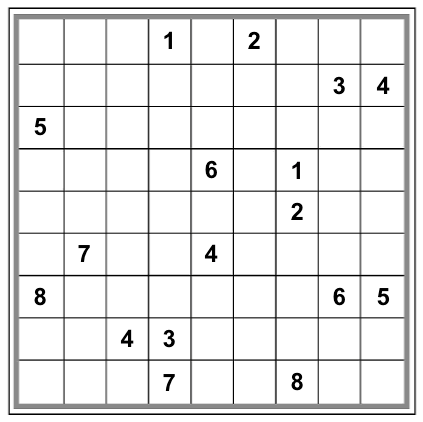So, in terms of my original puzzle, we would say that this particular meta-sudoku configuration is not a valid meta-sudoku puzzle: there is more than one possible meta-solution. (Namely, there are at least the four solutions above.)

---

How about the moose-shaped meta-sudoku? With 24 filled squares, brute force would look at 9²⁴ grids — that’s 80 thousand billion billion. From partial runs of my program in “counting” mode, I know it actually has somewhere between 480 billion and 87698 billion viable grids.

But my program quickly turned up many distinct solvable Sudoku grids for the moose configuration, which means that the moose, too, is not a valid meta-sudoku. Here are some of the distinctly solvable Sudokus you can form from the moose configuration:

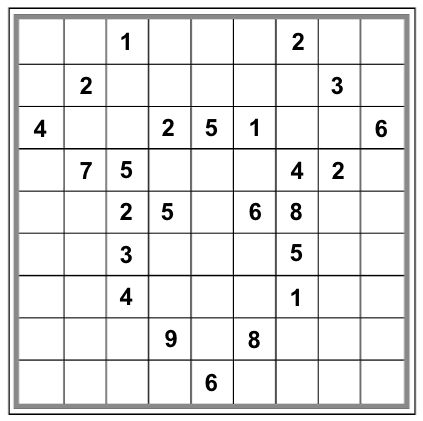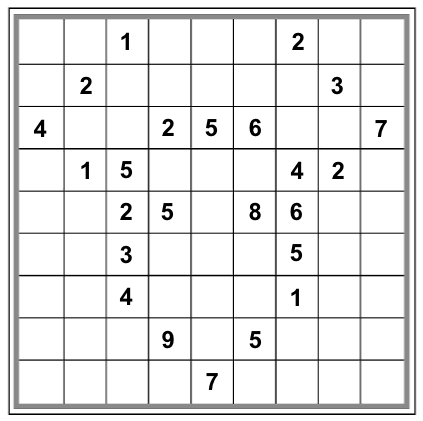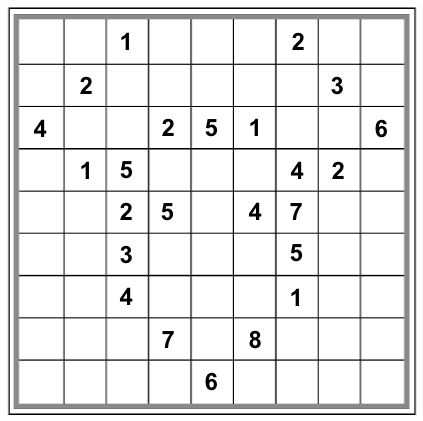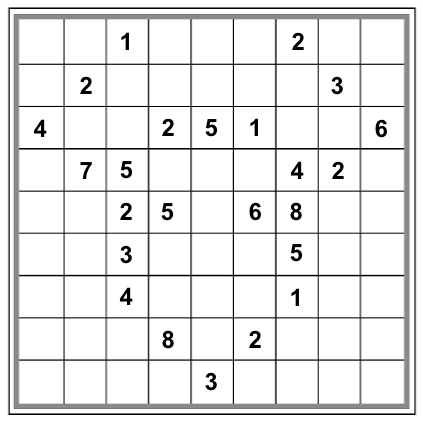I still don’t know if there exist any “meta-sudoku” configurations which are really “valid” in the sense of having only one distinct solution. If you find one, let me know!