Consider a plain represented by the unit square. On this plain we want to “peacefully encamp” two armies of point-sized soldiers — one army red and one army green. Each soldier “attacks” chess-queen-wise: horizontally, vertically, and diagonally in all directions. The puzzle is to maximize the size of the equal armies (equivalently, maximize the size of the smallest army), given the constraint that no pair of opposing soldiers can be placed attacking each other.

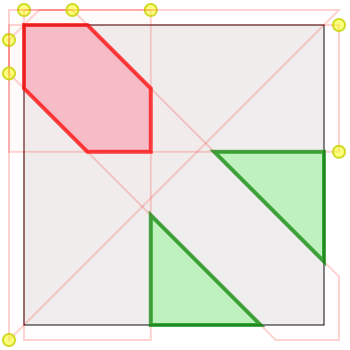
Previously on this blog: Back in 2014 I had conjectured that the optimum solution for two armies was the following. (Each region has size \(\left(1 - {\sqrt{3}\over 2}\right) \approx 0.13397\).) This morning I learned that I was very wrong about that!

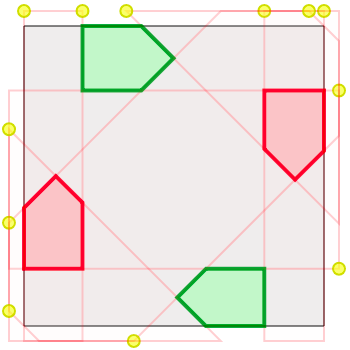
Last night I was noodling on this problem again (for the more-than-two-army case) and came up with this knight’s-move-inspired solution for 4 armies. Each home-plate-shaped region has size exactly 0.05.

In the above image, I used two colors to illustrate the four-army solution — so the four-army solution (also here) happens to double as a two-army solution of size 0.1. But what if we take that solution and rearrange the colors so that the friendly armies are next to each other instead of diametrically across the board from each other? I expected a modest increase, but after making the switch and jiggling it a bit, I arrived at this interesting configuration!

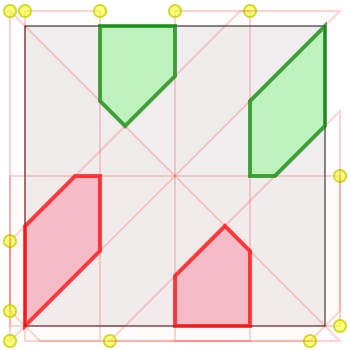The vertical lines divide the unit square into fourths; the slashing lines divide the sides of the unit square at the 1/3 and 2/3 marks. So each home-plate-sized region has size \(\frac{19}{288} \approx 0.06597\), and each slashing region has size \(\frac{23}{288} \approx 0.07986\), for a total army size of \(\frac{7}{48} \approx 0.1458\). Wow!

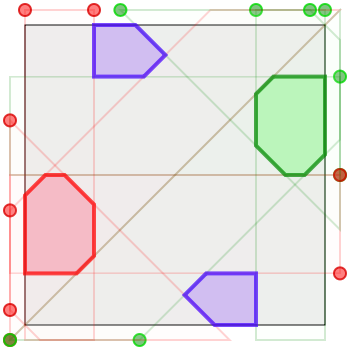
If we take the same four-army solution and color just two armies with the same color, then we get a three-army version. Jiggling that version arrives at these two solutions for three armies. The left-hand solution has army size \(\frac{1}{15} \approx 0.0667\); the better right-hand solution has army size \(\sim 0.0718\). I have not yet done the math to describe this solution algebraically.

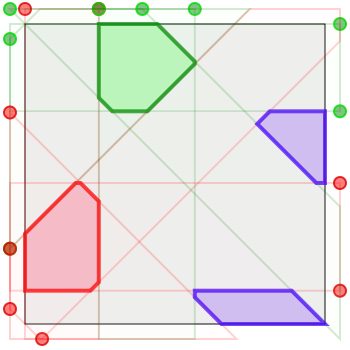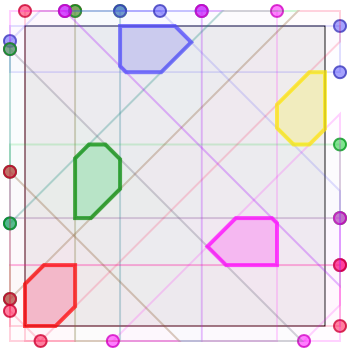
Here are two solutions for five armies. On the left, encampments of size \(\sim 0.0298\); on the right, encampments of size \(\frac{7}{225} \approx 0.0311\). Thanks to Benoît Jubin for doing the math on the latter! Benoît also informs me that you can very slightly widen the central encampment here to achieve encampments of size \(\sim 0.031188383\).

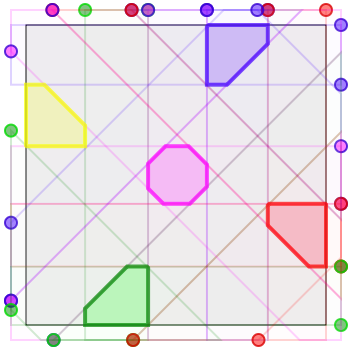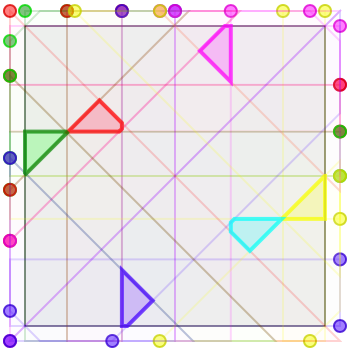
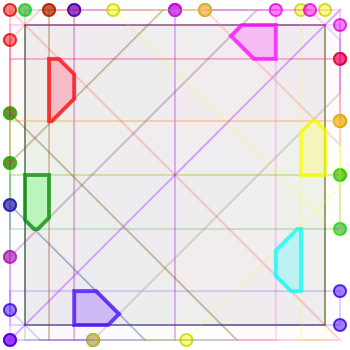
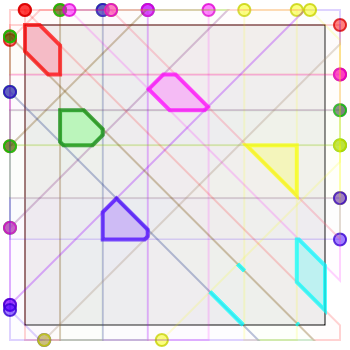
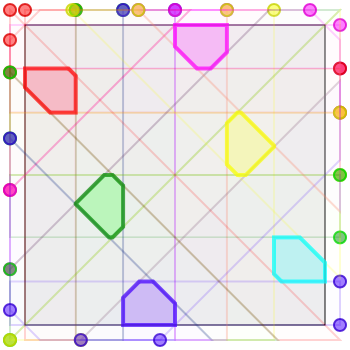
Here are four solutions for six armies, of sizes \(\sim 0.0104\), \(\sim 0.0133\), \(\sim 0.0140\), and (my best attempt) \(\sim 0.0211\), respectively. Again I haven’t done the math to describe these algebraically.

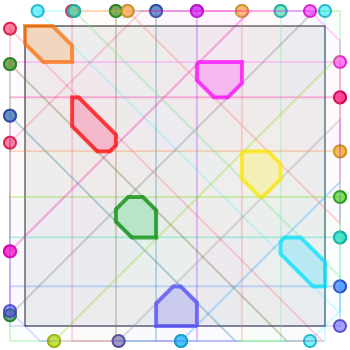
For seven armies, a solution of size \(\sim 0.0149\).

My best solution for eight armies is based on a solution to the eight queens puzzle; specifically, arrangement number 10 on Wikipedia’s list of the 12 distinct arrangements that solve the puzzle. Solutions based on the other 11 arrangements are available on my GitHub in a rough, unfinished form. This solution has armies of size \(\sim 0.0115\).
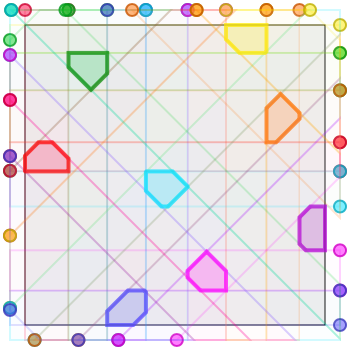