Polyomino strips, snakes, and ouroboroi

Previously on this blog: “Polycube snakes and ouroboroi” (2022-11-18).

Preparing to add the sequences from that post into OEIS, I realized to my surprise that most of the 2D analogues weren’t yet in OEIS either! There are several near-miss variations, though, involving the following concepts:

Polyominoes with holes (snakes versus strips)

Any polyomino divides the plane into one or more rookwise-connected regions. Two chess rooks are in different regions if one cannot reach the other in any number of rookwise moves without at some point passing through a cell of the polyomino. A polyomino which divides the plane into \(k+1\) regions is said to have \(k\) holes.

The smallest polyomino with a hole is the O-heptomino… which also happens to be a polyomino snake.

Two rooks divided by a snake

The polyomino divides the two pictured rooks from each other; therefore it is not a strip.

Miroslav Vicher refers to polyomino snakes without holes as strip polyominoes. Strip polyominoes are interesting if your main recreational interests in polyominoes are tilings and dissections, because holes pose a problem for those tasks. The 30 free heptomino-strips can tile a pretty 14x15 rectangle:

Image credit: Miroslav Vicher

but the 31 heptomino-snakes can’t tile any hole-free shape at all. Vicher notes that the 150 free nonomino-strips cannot tile any rectangle, either, because the nonomino depicted below has — not a hole, but what Vicher calls a cave.

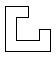
Image credit: Miroslav Vicher

Although the interior of the cave can be reached by a freely moving rook, it cannot be filled by any possible combination of snakes.

Vicher’s website often uses the shorthand “polystrip” to mean “strip polyomino”; but that’s unnecessarily confusing, given the established convention of using the suffix to identify the base form: polyomino, polyiamond, polyabolo, polyhex. We can speak also of strip polyiamonds, strip polyabolos, strip polyhexes; and snakes and ouroboroi of those forms as well.

OEIS sequences demonstrating the effect of holes include:

  • OEIS A049429 counts free d-dimensional polycubes
    • Summing across the first two columns of each row gives A000105, the count of free 2D polyominoes
    • Summing across the first three columns of each row gives A038119, the count of free 3D polycubes
    • Summing across the first four columns of each row gives A068870, the count of free 4D polyhypercubes
  • OEIS A000105 counts free polyominoes
  • OEIS A002013 counts free snake polyominoes
    • OEIS A333313 counts free snake polyominoes with no holes (i.e., strip polyominoes)
  • OEIS A038119 counts free polycubes

(Just to confuse matters, the title of OEIS A151514 and a 2009 comment on OEIS A002013 formerly used the term “strip” when they meant “snake.” But I submitted corrections and these are now fixed.)

Holes in 3D

There are at least two ways to define the 3D equivalent of a “strip” (resp. “a snake without holes”).

  • The simplest kind of 3D “hole” is a fully enclosed empty region from which a 3D rook could not escape by 3D-rookwise moves; this is also known as a “cavity.” The smallest polycube with such a cavity is also a snake: SRDRURDRUR wraps around all six faces of an empty cell, in the same way as the O-heptomino wraps around all four sides of an empty 2D cell. Similarly, the shortest polyhypercube snake with a cavity would use 15 hypercubes to wrap around all eight hyperfaces of an empty 4D cell; and so on.

  • A different kind of 3D hole is the “donut hole”: a tunnel through which you can pass a string, then connect the ends of the string to form a loop, such that the loop of string cannot escape to infinity no matter how much it wiggles. Of the three free eight-cube ouroboroi, one (the simplest) has a donut hole, and the other two don’t. Of the two chiral ten-cube ouroboroi, one has a donut hole, and the other (being the polycube equivalent of a horn torus) doesn’t.

  • My lovely wife pointed out the donut-hole possibility; I then further observed that some polycube ouroboroi have what I might call “pseudo-tunnels,” where the ouroboros itself actually does not circumnavigate the tunnel, but simply doubles back on itself. We can characterize these pseudo-tunnels by whether our loop of string can escape them by wiggling through corners, or whether it must wiggle through edges as well. I believe the smallest polycube ouroboros with an “edge-type pseudo-tunnel” is this quite appropriately shaped 22-cube construction:

Sam's heart-shaped ouroboros

A minor tweak gives a 24-cube ouroboros with a “corner-type pseudo-tunnel”; this can be reduced to a 22-cube ouroboros (see my followup post).

One-sided versus free polyominoes

Whenever we talk about the distinctness of d-dimensional shapes, we must clarify what kinds of rotations we’re permitting.

  • No rotations at all: “fixed” polyominoes
  • Rotations in d-space but no higher: “one-sided” polyominoes
  • Rotations through d+1-space: “two-sided” or “free” polyominoes

When counting “one-sided” 2D polyominoes, we don’t allow flipping them over through 3-space: mirror images are counted as distinct. Likewise, when counting “one-sided” 3D polycubes, we don’t allow flipping them through hyperspace: mirror images are counted as distinct. A polyform with distinct left- and right-handed variants is called “chiral”: its left- and right-handed variants are counted as two distinct one-sided polyforms, but identified as the same free polyform.

This notion of one-sidedness is different from my previous blog post’s notion of “directed snakes,” where I was distinguishing the snake’s head from its tail.

The mathematical term for that concept seems to be “rootedness,” although you might need some more verbiage to explain that a “rooted snake” must have its root actually at one of its ends, and not somewhere in the middle.

The following image shows just four free undirected polyomino snakes (the I, L, W, and Z pentominoes); but since the L and Z are chiral, we have a total of six one-sided undirected snakes in the left half of the image. Meanwhile, variants of the L and W produce six free directed/rooted snakes across the top half of the image; and the entire image shows nine examples of one-sided directed snakes. (Of course this is just a representative sampling of the total number of one-sided directed snake pentominoes.)

Chiral and directed snake pentominoes

OEIS sequences demonstrating the effect of chirality include:

Table of results (2D)

Here are my results for the 2D polyomino cases (source code). Columns corresponding to existing OEIS sequences are marked accordingly. OEIS sequences that did not exist prior to this blog post are italicized.

n Free strip polyominoes (A333313) Free non-ouroboros snakes (A002013) Free ouroboroi (A359706) One-sided strips (A359068) One-sided non-ouroboros snakes (A151514) One-sided ouroboroi (A359707)
1 1 1   1 1  
2 1 1   1 1  
3 2 2   2 2  
4 3 3 1 5 5 1
5 7 7   10 10  
6 13 13 0 24 24 0
7 30 31   52 53  
8 64 65 1 124 126 1
9 150 154   282 289  
10 338 347 1 668 686 1
11 794 824   1548 1604  
12 1836 1905 4 3654 3792 4
13 4313 4512   8533 8925  
14 10067 10546 7 20093 21051 11
15 23621 24935   47033 49638  
16 55313 58476 31 110533 116858 45
17 129647 138002   258807 275480  
18 303720 323894 95 607227 647573 178
19 711078 763172   1421055 1525113  
20 1665037 1790585 420 3329585 3580673 762
21 3894282 4213061   7785995 8423334  
22 9111343 9878541 1682 18221563 19755938 3309
23 21290577 23214728   42575336 46422915  
24 49770844 54393063 7544 99539106 108783480 14725
25 116206114 127687369   232398659 255359883  
26 271435025 298969219 33288 542864111 597932342 66323
27 633298969 701171557   1266567155 1402308318  
28 1478178004 1640683309 152022 2956342341 3281352516 302342
29 3446626028 3844724417   6893180336 7689369625  
30 8039424324 8991137036 696096 16078817198 17982241557 1391008
31 18734704111 21054243655   37469245219 42108302007  
32 43673728357 49211076053 3231001 87347384305 98422076879 6453950
33 101723730306 115161584232   203447081205 230322745835  

Table of results (3D)

Here’s a partial table of 3D polycube cases (source code). Columns corresponding to existing OEIS sequences are marked, as above.

The table below indicates the existence of two chiral pairs among the 10-cube ouroboroi. Can you find them? How about the three different ways to enclose a cavity with a 12-cube ouroboros (one mirror-symmetric, the other two forming a chiral pair)?

n Free non-ouroboros snakes (A363202) Free non-ouroboros snakes with cavities Free ouroboroi Free ouroboroi with cavities One-sided non-ouroboros snakes (A363201) One-sided non-ouroboros snakes with cavities One-sided ouroboroi One-sided ouroboroi with cavities
1 1       1      
2 1       1      
3 2       2      
4 4   1   5   1  
5 12       16      
6 34   1   54   1  
7 125       212      
8 450   3   827   3  
9 1780       3369      
10 7021   11   13653   13  
11 28521 4     56052 8    
12 115553 5 77 2 229004 10 122 3
13 472578 24     939935 48    
14 1927634 105 606 0 3843859 210 1115 0
15 7890893 485     15753903 970    
16 32221475 2098 6465 4 64380796 4196 12562 8
17 131812746 9381     263475472 18762    
18 538059836 40566 74314 23 1075780425 81132 147350 46
19 2198986587 178329     4397161320 356658    
20 8970624060 768163 907495 273 17939394036 1536321 1810165 545
21 36628143111 3334895     73251877235 6669790    
22 149328243327 14303573 11415061 2980 298646347226 28607136 22812552 5960
23 609238673619 61571929     1218453344740 123143833    

See also:

Posted 2022-12-08
math pretty-pictures puzzles