Polycube snakes and ouroboroi
PSA: Did you know that you can access all of JSTOR, and several other online archives, if you have a Wikipedia account of sufficient age with sufficiently many recent edits? Visit wikipedialibrary.wmflabs.org to learn more.
In the June 1981 issue of Scientific American (JSTOR; direct link for Wikipedia users) Martin Gardner’s “Mathematical Games” column is titled “The inspired geometrical symmetries of Scott Kim.” Readers of this blog will remember Scott Kim as the creator of many fantastic ambigrams: “Scott Kim’s rotational ambigrams for the Celebration of Mind” (2020-10-18). Most of Gardner’s column indeed focuses on that part of Kim’s oeuvre. But the bit that piqued my interest this week was the following space-filling puzzle:
First we must define a snake. It is a single connected chain of identical unit cubes joined at their faces in such a way that each cube (except for a cube at the end of a chain) is attached face-to-face to exactly two other cubes. The snake may twist in any possible direction, provided no internal cube abuts the face of any cube other than its two immediate neighbors. The snake may, however, twist so that any number of its cubes touch along edges or at corners. A polycube snake may be finite in length, having two end cubes that are each fastened to only one cube, or it may be finite and closed so that it has no ends. A snake may also have just one end and be infinite in length, or it may be infinite and endless in both directions.
We now ask a deceptively simple question. What is the smallest number of snakes needed to fill all space? We can put it another way: Imagine space to be completely packed with an infinite number of unit cubes. What is the smallest number of snakes into which it can be dissected by cutting along the planes that define the cubes?
[…] Kim has found a way of twisting four infinitely long one-ended snakes into a structure of interlocked helical shapes that fill all space. The method is too complicated to explain in a limited space; you will have to take my word that it can be done. […] Kim has conjectured that in a space of \(n\) dimensions the minimum number of snakes that completely fill it is \(2(n-1)\), but the guess is still a shaky one.
I’d love to see Kim’s space-filling quadruple-snake configuration — Gardner doesn’t show it, even when he reprinted this column with addenda in The Last Recreations (1997) and The Colossal Book of Mathematics (2001). I have asked Math StackExchange in case anyone there knows. Someone else is also interested:
- “Polycube Snakes” (Alaric Stephen, May 2017)
UPDATE, 2023-06-27: In March 2023 Scott told me his solution! Now it’s recorded on this blog as well: “Space-filling polycube snakes” (2023-06-27)
Enumerating polycube snakes
The number of polycubes of a given size, like the number of polyominoes, is well-studied: OEIS A000162. How many polycube snakes are there of a given size?
Every polycube of size less than 4 is a snake. At size 4, we already run into a fiddly difficulty! Certainly the I, L, and Z tetracubes, and the two “twists” that the Soma cube calls A and B, are snakes. But what about the square (smashboy)? Its head adjoins its tail, making it a non-snake if our rule is that no cube may adjoin any cube except its neighbors. But by Martin Gardner’s definition above, the square is a snake: each cube adjoins no more than two others. We might call the square tetromino a polycube ouroboros.
A checkerboard argument proves there are no polycube ouroboroi of odd sizes. There is one ouroboros of size 6, made by removing two opposite corners from a 2x2x2 arrangement (or equivalently, stacking two V-tricubes on top of each other). There are three ouroboroi of size 8; one, made by stacking two twists on top of each other, is shown below. And there are 13 ouroboroi of size 10.
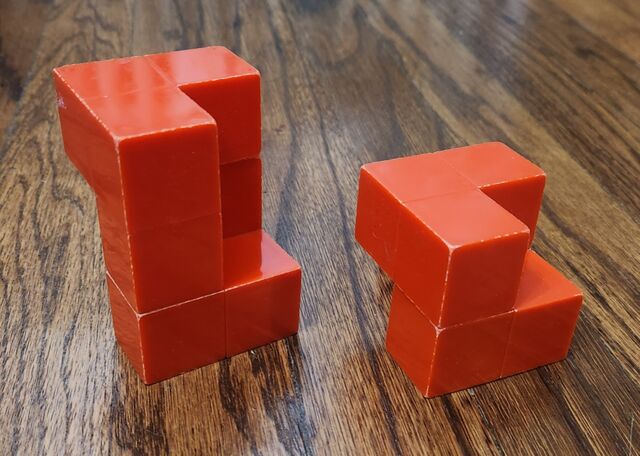
For a non-ouroboros, we have a choice to distinguish one of the two end cubes as the “head” (a “directed polycube snake”), or to leave them undifferentiated (an “undirected polycube snake”). For example, the L-tetromino corresponds to two distinguishable directed snakes: one with its head on the short leg of the L, and one with its head on the long leg. But the I-tetromino (four cubes in a straight line) corresponds to only one directed snake.
I suppose we could also consider “directed ouroboroi,” by designating the head and tail cubes
of an ouroboros; this would result in two directed hexacube ouroboroi, SRDRD and SRURU, and
the eight-cube ouroboros depicted above corresponds to no less than four directed
ouroboroi!
I wrote a quick-and-dirty C++20 program to enumerate polycube snakes and undirected ouroboroi (source code). It produced the following table:
| Cubes | Directed non-ouroboroi | Undirected non-ouroboroi | Undirected ouroboroi |
|---|---|---|---|
| 1 | 1 | 1 | |
| 2 | 1 | 1 | 0 |
| 3 | 2 | 2 | |
| 4 | 6 | 5 | 1 |
| 5 | 23 | 16 | |
| 6 | 93 | 54 | 1 |
| 7 | 386 | 212 | |
| 8 | 1590 | 827 | 3 |
| 9 | 6583 | 3369 | |
| 10 | 27046 | 13653 | 13 |
| 11 | 111460 | 56052 | |
| 12 | 456937 | 229004 | 122 |
| 13 | 1877277 | 939935 | |
| 14 | 7683372 | 3843859 | 1115 |
| 15 | 31497124 | 15753903 | |
| 16 | 128743825 | 64380796 | 12562 |
| 17 | 526907643 | 263475472 | |
| 18 | 2151488689 | 1075780425 | 147350 |
| 19 | 8794145222 | 4397161320 | |
| 20 | 35878493709 | 17939394036 | 1810165 |
| 21 | 146503034913 | 73251877235 | |
| 22 | 597291499318 | 298646347226 | 22812552 |
| 23 | 2436903747928 | 1218453344740 |
Notes on the C++ program
We can represent a snake using notation inspired by
Albie Fiore’s Shaping Rubik’s Snake (1981).
Peer down one end of the snake and move your eye along the segments, recording at each transition
whether you need to turn left, right, up, down, or straight (and rotating the whole snake
each time to keep the current cube in front of your eye).
In this notation the two tricube snakes are SS and SR;
the undirected tetracube snakes are SSS, SRS, SRL, SRU, SRD, and the ouroboros SRR;
and the hexacube ouroboros can be represented as SRDRD.
The above letter-strings are all in “canonical form”: they begin with S, and the
first turning we come to (if any) is always an R. It’s possible to represent the
V-tricube “non-canonically” as SL or SU or even LR, but that would be confusing,
so let’s not.
The undirected L-tetracube can be represented as either SRS (starting on the short leg)
or SSR (starting on the long leg); I arbitrarily choose the string that comes
first alphabetically as the unique representative of its equivalence class.
So, the program’s job is essentially to generate all possible \((n-1)\)-character letter-strings,
and then winnow out the ones that aren’t in canonical form, and then further winnow out the
ones that aren’t snakes (for example, SSRURU’s second cube has three neighbors). This produces
a list of directed snakes and/or ouroboroi. For non-ouroboroi, we must then compare the snake
to its own reversal to avoid double-counting it. De-duplicating ouroboroi, which have
no designated head or tail at all, is more tedious.
To generate the initial stock of strings_of_length(n),
I initially used a C++20 coroutine — a function returning a generator<string_view>
onto a string stored in the coroutine frame. This was one of my first forays
into coroutines, and I found it quite painless for this use-case.
The code for generator is given in
“Announcing Quuxplusone/coro” (2019-07-03).
The caveat here is that it would have been just as easy in this case not to use coroutines;
and when I factored out odometer(s) into its own function and got rid of the
then-trivial coroutine wrapper, things got 1% faster.
This was also the first time I’ve used C++20 std::span<T>, and again it seemed
like the right tool for the job; although I also have a nagging feeling that my
code went overboard on all the string_views and spans and maybe there could
have been a better way to organize it from the beginning.
To winnow out duplicate snakes,
at first I wrote a function string canonical_reversal(string_view) to actually
produce the reversal of a snake (for example, the reversal of SSR is SRS),
but eventually I realized that all we do is compare that reversal to the original
string and bail out if the reversal is alphabetically less — so we don’t actually
have to build the reversed string at all! Instead of
for each step i of the reversed snake:
compute the next letter L
RS[i] = L
finally, return (S <= RS)
we can simply do
for each step i of the reversed snake:
compute the next letter L
if L != S[i]:
return (S[i] < L)
return true
This not only saves memory accesses on RS, but also short-circuits quite a bit
of the loop.
My next optimization was to notice that no valid snake (except smashboy) can ever contain
the substrings RR, LL, UU, or DD; so any time our odometer algorithm creates
such a substring, we should “fast-forward” in constant time to the next string. Of course
we should also fast-forward any time we create a non-canonical letter-string, such as
SSLSS; we should skip straight to SRSSS in that case.
With these algorithmic optimizations, on my laptop, the above program can enumerate all 64,380,796 undirected sixteen-cube snakes (and all 12,562 ouroboroi) in just over a minute.
One more optimization is worthy of consideration: Each directed snake of length \(n+1\) can be constructed by appending one cube to the tail of some directed snake of length \(n\), and each undirected snake of length \(n+1\) can be constructed by appending one cube to the head or tail of some undirected non-ouroboros of length \(n\). So, to find the snakes of length 17, we wouldn’t have to run through all \(742\,803\,769\) letter-strings produced by our optimized odometer; we’d only have to check \(10\times 64\,380\,796 = 643\,807\,960\) or even \(5\times 128\,743\,825 = 643\,719\,125\) possibilities. However, the naïve way of doing this involves having one pass store all of the snakes of length \(n\) so that the next pass can use them to find snakes of length \(n+1\), and “storing all the snakes” doesn’t scale: for \(n=20\) the number of undirected non-ouroboroi is almost 18 billion. So I’m afraid I don’t see a good way to incorporate this idea.
See updated tables in this followup post:
- “Polyomino strips, snakes, and ouroboroi” (2022-12-08)
