In “Polycube snakes and ouroboroi” (2022-11-18), I quoted Martin Gardner (June 1981) on the topic of filling space with polycube snakes:

We now ask a deceptively simple question. What is the smallest number of snakes needed to fill all space? We can put it another way: Imagine space to be completely packed with an infinite number of unit cubes. What is the smallest number of snakes into which it can be dissected by cutting along the planes that define the cubes?

[… Scott] Kim has found a way of twisting four infinitely long one-ended snakes into a structure of interlocked helical shapes that fill all space. The method is too complicated to explain in a limited space; you will have to take my word that it can be done. […] Kim has conjectured that in a space of \(n\) dimensions the minimum number of snakes that completely fill it is \(2(n-1)\), but the guess is still a shaky one.

Back in March, I contacted Scott Kim through the Gathering 4 Gardner meetup and asked if he recalled his solution. Of course he did! Scott quickly put together a diagram (here) and presented his solution at a subsequent meetup (YouTube).

Scott writes:

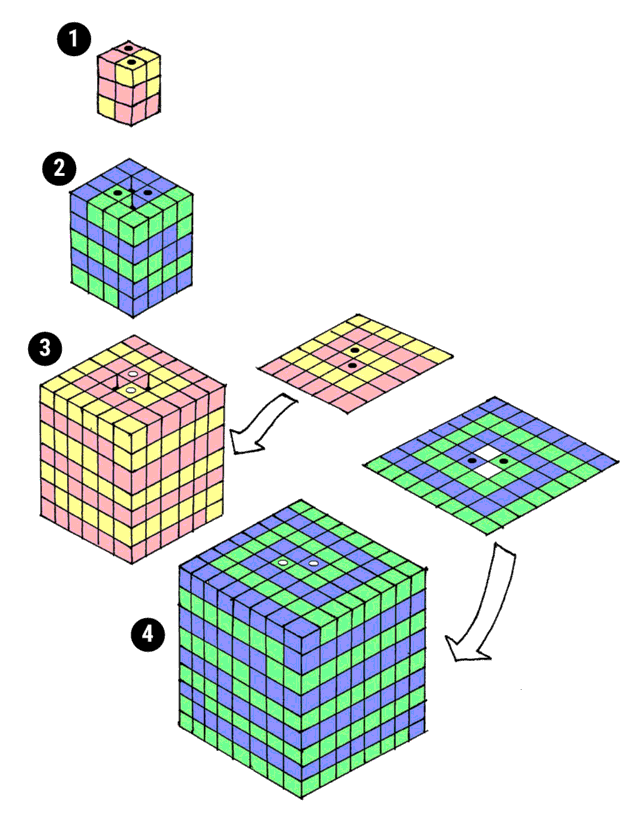
Shown here is a space-filling solution with 4 snakes.

1. The red and yellow snakes spiral around each other to form a 2x2x3 solid (one cube higher than wide), ending at the two top squares marked with black dots.

2. Then the green and blue snakes coil around each other to build a shell enclosing the red and yellow snakes, starting in the middle of the bottom, spiraling out, climbing up the walls, spiraling in, and stopping one cube short of closing the shell.

3. The process then repeats. First, the ends of the red and yellow snakes poke up through the holes in the blue-green shell (see cubes marked with white dots) and spiral down to form a shell with two holes at the bottom for the green and blue snakes to escape.

4. Then the blue and green snakes poke up through the holes and spiral down to form a shell with no holes at the top, but two holes at the bottom. The process continues, building red-yellow and blue-green shells, alternately up and down.

What’s remarkable is that the diagonal of kinks that run down the shell always end at the right place to neatly finish the structure with no mess. Please email me if you have insights at scott@scottkim.com.

I made a Lego version of Scott’s solution. Shown fully disassembled (with bonus Welsh-terrier blur); partly assembled; and completely assembled.

That completely resolves my original desire to learn Scott Kim’s four-snake space-filling pattern. The original open problems remain:

• Can you fill space with only three snakes?

• Can you fill 4-space with six polyhypercube snakes, 5-space with eight snakes, and so on?