The other day I was pointed at this excellent set of template-metaprogramming exercises:

• “C++ Metaprogramming Exercises Vol. I” (Ondřej Slámečka, March 2021)

The exercises build gradually, from Prepend and Append, to RemoveFirst and RemoveAll, to Sort. The only things I’d have done differently in that sequence are to include PopFront (which is easier) before PopBack (which, unless I’m missing something, is harder); and include Iota (i.e. std::make_index_sequence) after Length.

Now, one way to implement Sort is to implement a selection sort from scratch by combining Min, RemoveFirst, and Prepend. In fact that’s how Ondřej’s sample solution does it.

template<class> struct Sort;
template<> struct Sort<Vector<>> : TypeIdentity<Vector<>> {};
template<int... Is> struct Sort<Vector<Is...>> {
  using Min = Min<Vector<Is...>>;
  using Tail = RemoveFirst<Min::value, Vector<Is...>>::type;
  using type = Prepend<Min::value, typename Sort<Tail>::type>::type;
};

But since as a Professional Software Engineer™ I have a (possibly irrational) allergy to writing sort algorithms by hand, and since C++20 gives us a constexpr-friendly std::sort, the way that first occurred to me was simply to do the sorting in value-space using std::sort, and then lower the answer back down into type-space. So that’s how I did it (Godbolt):

template<class> struct Sort;
template<int... Is> struct Sort<Vector<Is...>> {
  static constexpr int GetNthElement(int i) {
    int arr[] = {Is...};
    std::ranges::sort(arr);
    return arr[i];
  }
  template<class> struct Helper;
  template<int... Indices> struct Helper<Vector<Indices...>> {
    using type = Vector<GetNthElement(Indices)...>;
  };
  using type = Helper<Iota<sizeof...(Is)>>::type;
};

static_assert(std::same_as<Sort<Vector<2,4,1,3>>::type, Vector<1,2,3,4>>);

I don’t know any good way to operate on a whole pack of Is... in value-space and then “return” them into type-space as Vector<Is...>; but I do know the trick above, which is to return each element of the result individually and then glue those \(n\) individual constexpr results back together as Vector<GetNthElement(Indices)...>. This ends up doing the constexpr work \(n\) times instead of just once, so we expect it to be super inefficient: as shown, this is an \(O(n^2 \log n)\) sorting algorithm!

But the name of GetNthElement hints that we can replace std::ranges::sort(arr) with std::ranges::nth_element(arr, arr+i). This makes the whole sorting operation \(O(n^2)\), just like the open-coded selection sort above.

The good way I was missing has been pointed out by alert reader “Chlorie.” Basically it’s to return an array, capture it in a constexpr variable, and then use Vector<arr[Indices]...>. See “Sorting at compile time, part 2” (2024-02-20).

Compile-time benchmark

Which compile-time sort is faster? Naïvely, I expect the constexpr version to be faster, because it avoids “recursive templates”; see “Iteration is better than recursion” (2018-07-23). On the other hand, its “gluing individual elements” trick causes it to do the same work \(n\) times in a row, which sounds slow, even if each individual computation is constexpr and therefore fast. But, back on the first hand, we know that both versions have the same asymptotic complexity — even the dumbest version, calling std::ranges::sort \(n\) times, is only off by a factor of \(\log n\) (which, “for most practical purposes, is less than 64”). And we expect the compiler to do better at direct value-space constexpr evaluation than at instantiating \(O(n)\) intermediate class types. So I clearly cannot choose the implementation in front of you!

We also expect the compiler to do better at simple constexpr evaluation than at instantiating \(O(n)\) intermediate class types. But, on the other hand, std::sort and std::nth_element are hardly “simple” functions! Our STL vendor (whether it’s libc++, libstdc++, or Microsoft) will send those functions through several layers of indirection and customization — even a simple operation like dereferencing the raw pointer arr+i might cause the instantiation of std::iter_move and/or std::iter_swap. And if we use std::ranges::sort, then we’re touching everything from std::ranges::random_access_range to decltype(std::ranges::iter_move)::operator(). There’s no world in which std::ranges::sort is less complicated than our simple open-coded selection sort. So I clearly cannot choose the implementation in front of me!

Fortunately, C++ programmers have spent the last few years building up an immunity to long compile times.

To satisfy my curiosity, I wrote a little benchmark for this (here). The benchmark generates several random lists of integers of a given length \(n\) and calls Sort on them, then static_asserts that the output is what we expect.

The benchmark script compares selection sort against four minor variations of the constexpr solution: std::sort, std::ranges::sort, std::nth_element, and std::ranges::nth_element. It also compares what happens if Vector<Is...> is a hand-coded empty struct, versus an alias for std::integer_sequence<int, Is...>. We always include the <algorithm> header, even when it’s not needed. We always compile with -O2, since that’s what we’d expect in production.

Benchmark results

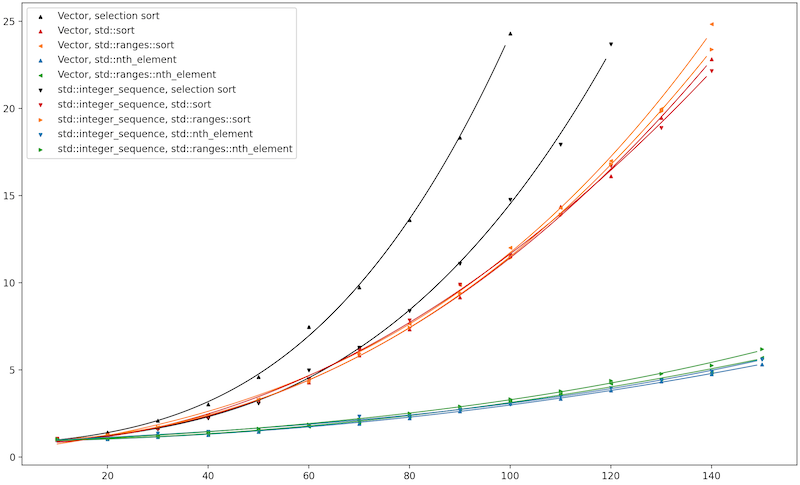
Here’s Clang trunk (the future Clang 19) with libc++, running on my MacBook.

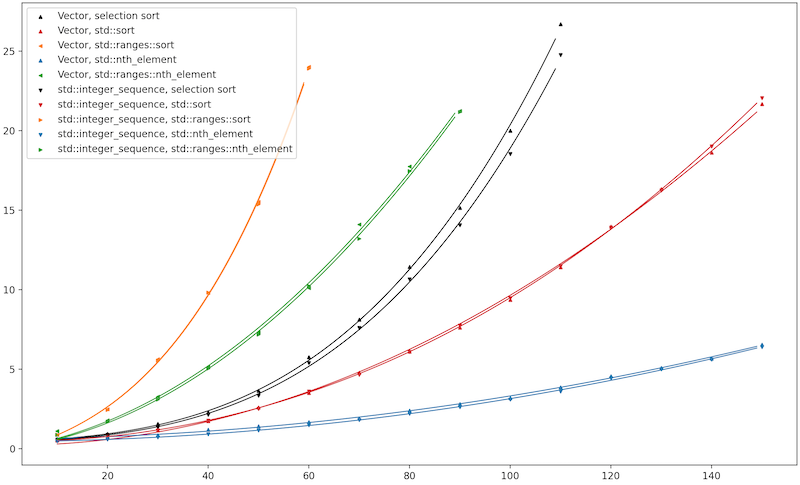
Here’s GCC 12.2 with libstdc++, running on RHEL 7.1.

I don’t have the ability to run this benchmark on MSVC, but if you do, please send me your results! Get my Python script here.

Observation #1: The constexpr-STL-algorithm version really doesn’t care whether you use std::integer_sequence or Vector. This actually surprised me a little bit, because the constexpr version is the one that uses Iota, and I expected my hand-rolled Iota to be slower than the STL vendor’s make_integer_sequence (which takes advantage of the compiler’s builtin __make_integer_seq). On such small inputs, though, I can see how the speed of Iota is the least of our worries.

Observation #2: Below the two lines for selection sort, we see distinctive curves for \(O(n^2\log n)\) std::sort and \(O(n^2)\) std::nth_element. As predicted, nth_element handily beats sort. This also gives a vendor-independent answer to my biggest question: Is constexpr-evaluated std::sort faster than a hand-metaprogrammed selection sort? Yes, constexpr beats metaprogramming.

Observation #3: On Clang/libc++, the Classic and Ranges algorithms are extremely similar in performance. On GCC/libstdc++, the Ranges algorithms take a huge penalty. At first I chalked this up to how on libc++ the guts of std::sort and std::ranges::sort are literally the same template, parameterized by an _AlgPolicy. (At the LLVM Dev Meeting in October 2023, Konstantin Varlamov gave a 20-minute talk touching on this. Obviously in 20 minutes one can’t go deep into the details; but he did claim that this design is unique to libc++. So this was on my mind already.)

However, libstdc++’s std::ranges::sort is also merely a thin wrapper around std::sort. It boils down to this:

It operator()(It first, Sentinel last, Comp comp = {}, Proj proj = {}) const {
  auto lasti = std::ranges::next(first, last);
  std::sort(first, lasti, detail::make_comparator_by_pasting_together(comp, proj));
  return lasti;
}

So if there’s a slowness to instantiating or evaluating this, it must be in the part that creates the comparator by pasting together std::ranges::less and std::identity to come up with a type whose behavior one could summarize as “std::less<int>, but slower.” Both libc++ and libstdc++ need to do that pasting-together, so why should libstdc++ be so much worse?… Well, libc++ optimizes the “99% case” where Proj is std::identity. libstdc++, as far as I can tell as of this writing, does not. So that’s why libstdc++’s std::ranges::sort(first, last) is vastly slower than their std::sort(first, last) — every call to the comparator turns into three or more calls to std::invoke!

In short, libstdc++’s Ranges algorithms suffer a huge constexpr penalty right now; but maybe they could easily fix that, by adding the same special case we see in libc++. For the time being, if your code uses STL algorithms at constexpr time, all else being equal, you should prefer std over std::ranges. In fact I’d give this advice to ordinary runtime code, too. In non-generic code that doesn’t need Ranges’ arcane features, why pay their cost?

See the followup for a better faster solution:

• “Sorting at compile time, part 2” (2024-02-20)