Yesterday, in “Sorting integer_sequence at compile time” (2024-02-19), I wrote:

I don’t know any good way to operate on a whole pack of Is... in value-space and then “return” them into type-space as Vector<Is...>.

So I had written a helper function to get each individual element of the result one by one, like this:

template<class> struct Sort;
template<int... Is> struct Sort<Vector<Is...>> {
  static constexpr int GetNthElement(int i) {
    int arr[] = {Is...};
    std::ranges::sort(arr);
    return arr[i];
  }
  template<class> struct Helper;
  template<int... Indices> struct Helper<Vector<Indices...>> {
    using type = Vector<GetNthElement(Indices)...>;
  };
  using type = Helper<Iota<sizeof...(Is)>>::type;
};

Alert reader “Chlorie” writes in to tell me the proper approach. We just need our helper to return a std::array of all the elements at once, and then — still — use a pack-expansion to unpack the elements out of that constexpr std::array and into Vector’s template argument list. (Here we use std::array, not int[], despite my usual advice, because we need something that can be returned from a function.) Godbolt:

template<int N> struct Array { int data[N]; };

template<class> struct Sort;
template<int... Is> struct Sort<Vector<Is...>> {
  static constexpr auto sorted = []() {
    Array<sizeof...(Is)> arr = {Is...};
    std::ranges::sort(arr.data);
    return arr;
  }();

  template<class> struct Helper;
  template<int... Indices> struct Helper<Vector<Indices...>> {
    using type = Vector<sorted.data[Indices]...>;
  };
  using type = Helper<Iota<sizeof...(Is)>>::type;
};

Now that sort is called only once, we have a truly \(O(n\log n)\) compile-time sorting operation.

Updated compile-time benchmark

Yesterday’s benchmark is still here; but I’ve updated it to include Chlorie’s proper \(O(n\log n)\) constexpr solution, using both std::sort and std::ranges::sort.

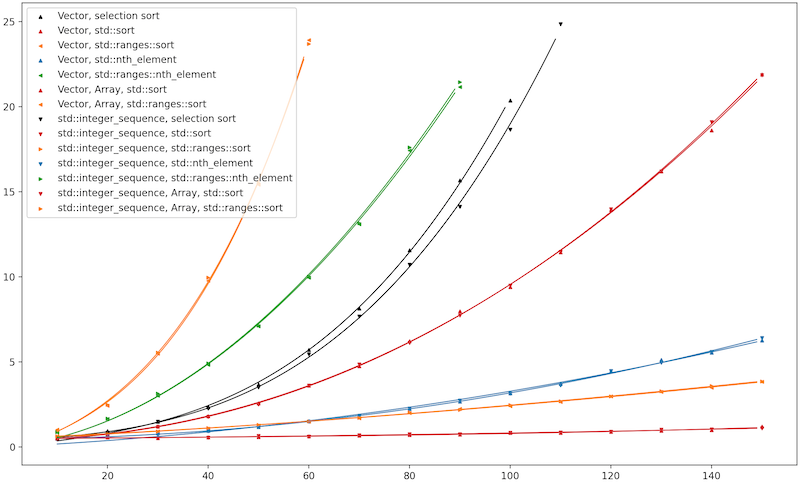
Here’s Clang trunk (the future Clang 19) with libc++, running on my MacBook. The new solutions are the orange and red lines closest to the X-axis. The orange and red lines higher up (unchanged from yesterday’s graph) are yesterday’s std::sort and std::ranges::sort solutions, which do basically \(n\) times as much work as today’s solutions.

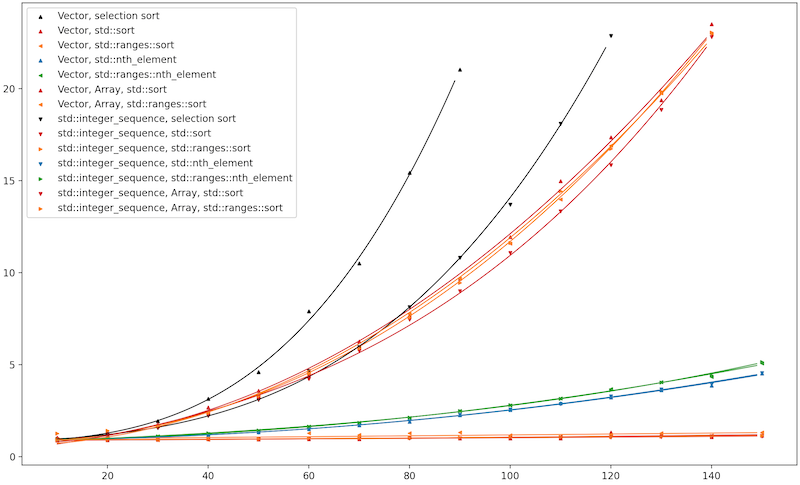
Here’s GCC 12.2 with libstdc++, running on RHEL 7.1. There’s still a noticeable compile-time-perf difference between libstdc++’s sort and ranges::sort, but even ranges::sort (in orange) now wins handily against yesterday’s recursive-template selection sort (in black).