Discrete Peaceful Encampments
Over the past couple of days I’ve posted variations on “Peaceful Encampments” as puzzles on StackExchange, to try to drum up some interest in them. I’ve learned that puzzlers greatly prefer discrete puzzles (queens on a chessboard) over continuous puzzles (such as the original “Peaceful Encampments” as seen on this blog): my discrete puzzles have gotten quick and accurate answers, whereas my original continuous version is languishing.
You have 9 white queens and 9 black queens. Place all these pieces onto a normal 8x8 chessboard in such a way that no white queen threatens a black queen (nor vice versa).
Today, player three enters the game!:
You have 4 white queens, 4 black queens, and 4 red queens. Place all these pieces onto a normal 8x8 chessboard in such a way that no white queen threatens a black queen, no black queen threatens a red queen, and no red queen threatens a white queen (nor vice versa).
I’ve written a C++ program to brute-force the maximum number of queens that can be placed peacefully on an NxN chessboard in the 2-army and 3-army cases. Much of the search space can be short-circuited, similarly to my meta-sudoku brute-forcer as seen on this blog (October 2018).
For two armies, the sequence of solutions is OEIS A250000:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(n) | 0 | 0 | 1 | 2 | 4 | 5 | 7 | 9 | 12 | 14 | 17 | 21 | 24 | 28 | 32 |
(That is, on a 4x4 chessboard you can fit peacefully 2 white and 2 black queens; on a 5x5 chessboard you can fit peacefully 4 white and 4 black queens; and so on.)
For three armies, the sequence was not found in the OEIS when this blog post first went up, but as of 2019-10-18, it’s OEIS A328283. Thanks to Dmitry Kamenetsky for adding it to the OEIS, and for writing a fast Java program to discover best-known (though not necessarily best) solutions!
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(n) | 0 | 0 | 0 | 1 | 1 | 2 | 3 | 4 | 5 | 7* | 8* | 10* | 12* | 14* | 16* | 18* |
(That is, on a 7x7 chessboard you can fit peacefully 3 white, 3 black, and 3 red queens; on an 8x8 chessboard you can fit peacefully 4 white, 4 black, and 4 red queens; and so on.)
Numbers with asterisks are best known solutions but not necessarily the best possible.
Here are my solutions, for the record:
4x4: 2 white, 1 black, 1 red (verified best)
.W..
...W
B...
..R.
5x5: 4 white, 2 black, 1 red (verified best)
WW...
...BB
.W...
W....
..R..
6x6: 3 white, 3 black, 2 red (verified best)
W.....
..B..B
.....B
......
WW....
...RR.
7x7: 4 white, 4 black, 3 red (verified best)
..WW...
..W....
......R
....W..
BB.....
BB.....
.....RR
8x8: 6 white, 5 black, 4 red (verified best)
..RR....
..RR....
......WW
.......W
.B......
BB......
BB......
.....WWW
9x9: 7 white, 6 black, 5 red (verified best)
..RRR....
..RR.....
.......BB
........B
.W.......
WW.......
WW.......
WW.......
......BBB
10x10: 8 white, 7 black, 7 red
...RR.....
...RRR....
...RR.....
........BB
.........B
..........
.WW.......
WWW.......
WWW.......
......BBBB
11x11: 10 white, 9 black, 8 red
...BBB.....
...BBB.....
...BB......
.........WW
..........W
......B....
.RR........
RRR........
RRR........
.......WWW.
.......WWWW
12x12: 11 white, 10 black, 10 red
...RR.......
...RRR......
...RRR......
...RR.......
.........BBB
..........BB
...........B
.WW.........
WWW.........
WWW.........
WWW.........
.......BBBB.
13x13: 12 white, 12 black, 12 red
...RR........
...RRR.......
...RRRR......
...RRR.......
..........WWW
..........WWW
...........WW
..B..........
.BB..........
BBB..........
BBB..........
BBB..........
........WWWW.
14x14: 14 white, 14 black, 14 red
...RRR........
...RRRR.......
...RRRR.......
...RRR........
...........WWW
...........WWW
............WW
.............W
.BB...........
BBB...........
BBB...........
BBB...........
BBB...........
........WWWWW.
15x15: 17 white, 16 black, 16 red
....RRRR.......
....RRRRR......
....RRRR.......
....RRR........
............WWW
.............WW
..............W
...............
..B............
.BBB...........
BBBB...........
BBBB...........
BBBB...........
.........WWWWW.
.........WWWWWW
16x16: 19 white, 18 black, 18 red
....RRR.........
....RRRR........
....RRRRR.......
....RRRR........
.....RR.........
............WWWW
.............WWW
..............WW
...B............
..BB............
.BBB............
BBBB............
BBBB............
BBBB............
..........WWWWW.
...........WWWWW
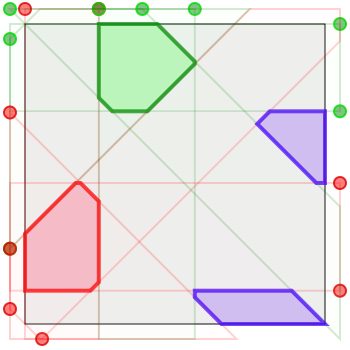
Notice the similarity between my conjectured 8x8-and-larger solutions and my conjectured solution to the continuous “Peaceful Encampments” puzzle for three armies:
 |
For more thorough treatment of this problem, see:
-
“Discrete Peaceful Encampments, with tables” (2019-10-18)
-
“Discrete Peaceful Encampments, Bernie Sanders version” (2020-03-21)
