The Fourth Dimension and the Bible (1922)
I just finished reading William A. Granville’s The Fourth Dimension and the Bible (1922). It’s quite mind-bending! I don’t mean the Biblical stuff (which is all quite a stretch), but specifically Granville’s mathematical examples, several of which were completely new to me.
Any reader of Flatland (Edwin Abbott, 1884) knows the basics:
-
How a cube passing through a plane casts “cross-sections” that may be squares, triangles, or hexagons depending on its angle.
-
How a Flatlander’s eye receives impressions in only one dimension.
-
How a Linelander keeps the same two neighbors for life, being unable to pass either of them.
-
How the three-dimensional cross-section of a fourth-dimensional being could appear within a locked room, or touch a point on the interior of a three-dimensional object without puncturing or intersecting the object’s surface.
A fourth-dimensional being could also undo a knot in a three-dimensional rope, bringing one portion of the rope past another portion — not “through” but “past” — by means of lifting that portion temporarily into the fourth dimension. Page 50:
Our knots would therefore be useless in four-dimensional space. Evidently our chains would also be useless because the links in them could be separated without breaking.
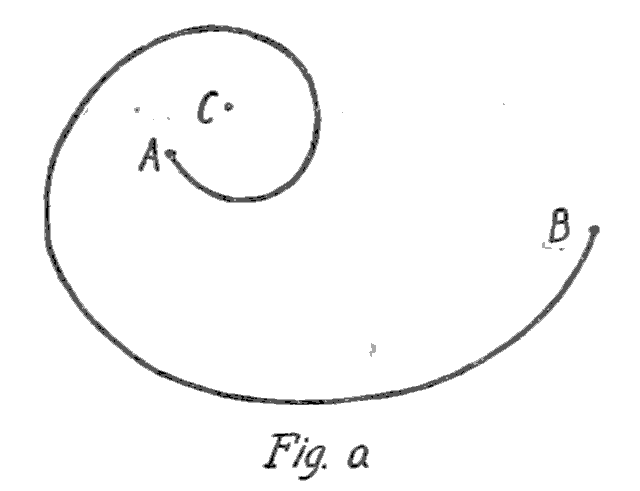
Corresponding to this in Flatland would be a cord fastened at \(A\) and \(B\) and making a loop around, say, \(C\).
This loop could not be unwound by a Flatlander, but one of us could do it by simply lifting that part of the cord composing the loop into the third dimension, stretching it out, and then replacing it in the plane.
I’d never particularly considered this idea of Flatland knots, or the impossibility of unlooping the cord from around \(C\). It makes me strangely anxious.
A few pages further on, Chapter 6 discusses “Rotation of Symmetric Configurations.”
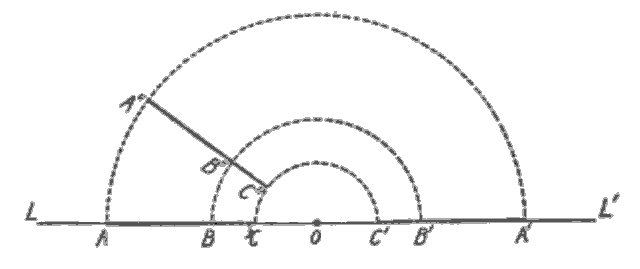
Let \(ABC\) and \(A'B'C'\) be two line [segments] in Lineland \(LL'\), the points \(A,B,C\) and \(A',B',C'\) respectively being arranged in the same order and so located such that \(AB=A'B'\), \(BC=B'C'\). One line may then be made to coincide with the other by simply sliding […] This could be done by a Linelander.
Let us now consider the two lines \(ABC\) and \(C'B'A'\), in which the corresponding points are arranged in the reverse order. In this case one cannot, by sliding it along \(LL'\), be made to coincide with the other so that \(A\) shall coincide with \(A'\), \(B\) with \(B'\), and \(C\) with \(C'\), and a Linelander could not conceive of any other way in which it might be done. A Flatlander, however, or one of us, would at once observe that the corresponding points could be brought into coincidence by rotating one of the lines about \(O\) in the plane of the page, \(O\) being the center of \(CC'\). […]
Roughly stated, the line \(ABC\) may be taken up into Flatland, turned over, and put down again on the line \(C'B'A'\). While this rotation was taking place the moving line, as in the position \(A''B''C''\), would be invisible to the Linelanders living in \(LL'\) because it would be outside of their world; the whole process would appear to them as a miracle.
Granville lifts the analogy from one dimension to two dimensions:
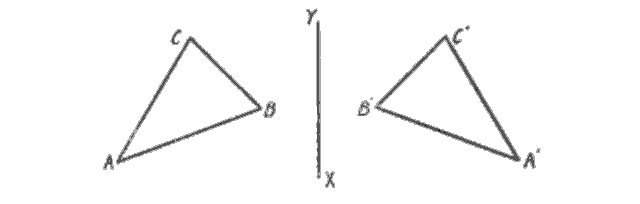
Let us now consider the two triangles \(ABC\) and \(A'B'C'\), in which as before \(AB = A'B'\), \(BC = B'C'\), and \(CA = C'A'\), but with their corresponding sides arranged in the reverse order. In this case the one triangle cannot, by sliding it along in the plane, be made to coincide with the other, and a Flatlander could not conceive of any other way in which it might be done.
A three-dimensional mathematician would observe, however, that the two triangles \(ABC\) and \(A'B'C'\) are symmetrical with respect to the line \(XY\) (corresponding points on the two triangles being located on the same perpendicular to \(XY\) and at equal distances from it), and that they can be brought into coincidence by rotating one (with the plane in which it lies) about the axis of symmetry \(XY\) thru three-dimensional space until it coincides with the other. That is, one triangle must be taken up into our space, turned over, and put down on the other. To Flatlanders this operation would be an unsolvable mystery.
And thence into three dimensions:
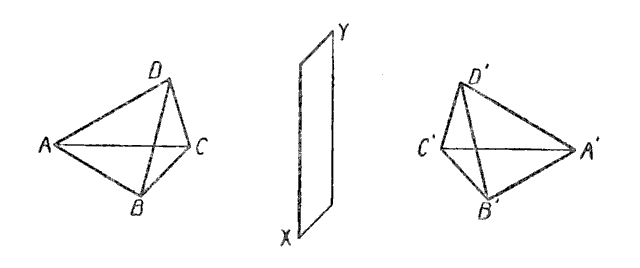
Let us now consider the two tetrahedrons \(ABCD\) and \(A'B'C'D'\) in which, as before, all the faces of one are equal to the corresponding faces of the other, but arranged in the reverse order. No amount of manipulation will now enable us to bring the two tetrahedrons into coincidence, and no human being can conceive of any way in which it can be done. This task is as impossible to us as was the task of the Linelander to bring the symmetrical lines \(ABC\) and \(C'B'A'\) into coincidence (p. 54) or the task of the Flatlander to make the two symmetrical triangles \(ABC\) and \(A'B'C'\) coincide (p. 56).
Mathematicians of the highest standing, however, have proven that it can be done in four-dimensional space by rotating one of the tetrahedrons about their plane of symmetry \(XY\) (corresponding points of the two tetrahedrons being located on the same perpendicular to \(XY\) and at equal distances from it) — a kind of rotation that is impossible in our space of three dimensions. Or, stating it roughly, one of the tetrahedrons must be taken up into space of four dimensions, turned over, and then brought back into coincidence with the other.
When we rotate the triangle \(ABC\) through the third dimension, no part of the triangle remains in Flatland; yet we can picture the two-dimensional triangular “shadow” that would be cast into Flatland by a light above and perpendicular to Flatland’s plane. (It may help to imagine a colored shadow, such that the points of the triangle further from the plane cast redder shadows, and the closer points cast bluer shadows.) Notice that halfway through \(ABC\)’s rotation, when the triangle’s own plane is perpendicular to Flatland’s, the triangle’s shadow is momentarily reduced to a one-dimensional line (collinear with the line of symmetry \(XY\)).
When we rotate the tetrahedron \(ABCD\) through the fourth dimension, no part of the tetrahedron remains in Spaceland; yet we can picture the tetrahedral “shadow” that would be cast into Spaceland by a light beyond and perpendicular to Spaceland’s space. Halfway through \(ABCD\)’s rotation, when the tetrahedron’s own space is perpendicular to Spaceland’s, the tetrahedron’s shadow would be momentarily reduced to a two-dimensional triangle (coplanar with the plane of symmetry \(XY\)).
During the most recent Celebration of Mind, I happened across a neat “Flatland Simulator” written in JavaScript by Zachary Fletcher. The idea is to show what A. Square would see, in a real Flatland environment. Play it here!
This particular simulation, in true Flatlander style, omits any depiction of Women or the Lower Classes; and its Regular Polygons swoop around rotating in a frankly vulgar fashion. The grayscale is also a bit low-contrast for my eyes; it would be fun to add a toggle demonstrating the visual impact of Chromatism. Finally, I wish it were possible to toggle off the two-dimensional “spoiler” diagram below the one-dimensional visualization. I’ve forked the repo with the intent of modifying Fletcher’s (GPL’ed) code; maybe one of these days I’ll get around to it.